Las figuras geométricas componen todo lo que está alrededor
de nosotros. Pueden ser bidimensionales, como la pantalla de tu computadora, y
tridimensionales, como una pelota. Cada figura geométrica tiene sus propiedades
que la hacen diferente de otras figuras. Sin embargo, las figuras geométricas
pueden compartir propiedades con otras, lo que requiere describirlas más
detalladamente para distinguirlas de otras figuras.


CIRCULO
El círculo es una figura geométrica que se realiza trazando
una curva que está siempre a la misma distancia de un punto que llamamos
centro.
La línea que bordea al círculo se llama circunferencia.
Es importante saber que la diferencia entre la
circunferencia y el círculo es que la circunferencia es lo que rodea al
círculo, y el círculo es todo lo que contiene la circunferencia.

El centro del círculo (o centro de la circunferencia, mejor
dicho) es el punto del cual equidistan todos los puntos.

El radio es un segmento del círculo que une el centro con
cualquier punto de la circunferencia.

El
diámetro es un segmento del círculo que une dos puntos de la circunferencia
pasando por el centro y divide al círculo en dos partes iguales. El diámetro es
dos veces el radio, o mejor dicho, el radio es la mitad del diámetro.

La cuerda es un segmento del círculo que une dos puntos de la
circunferencia pero lo que le diferencia del diámetro es que no pasa por el
centro del círculo.

CUADRADO
El cuadrado es un polígono con cuatro lados (cuadrilátero)
iguales. Sus cuatro ángulos interiores también son iguales y rectos (de 90º
cada uno).

- Lados: el cuadrado tiene cuatro lados (a) iguales y paralelos dos a dos.
- Ángulos: tiene cuatro ángulos (α) iguales y rectos de 90º (π/2 radianes). Los ángulos interiores, como en todo cuadrilátero, suman 360º (2π radianes).
- Diagonales: las diagonales son segmentos que unen los vértices opuestos. Tiene dos diagonales (D1 y D2) iguales y perpendiculares. Se cortan en el centro del cuadrado. Las diagonales son las bisectrices de los ángulos. También son ejes de simetría.
- Ejes de simetría: son líneas imaginarias que dividen el cuadrado en dos partes simétricas respecto a dicho eje. Tiene cuatro ejes de simetría (E1, E2, E3 y E4).
El cuadrado es un caso particular del rectángulo, siendo los
pares de lados iguales. También es un caso particular del rombo, con los pares
de ángulos iguales y rectos (de 90º).

Diagonal del cuadrado
La diagonal del cuadrado (D) se puede calcular a partir de la longitud de los lados. La fórmula para calcular la diagonal es:
Fórmula de la diagonal del cuadrado

Ésta fórmula se obtiene directamente de la ley del paralelogramo.
También podría obtenerse también a partir del teorema de Pitágoras, ya que dos lados (a) consecutivos del cuadrado y la diagonal forman un triángulo rectángulo.

Área del cuadrado
El área del cuadrado se calcula a partir de uno de sus lados (a). Es el producto de la base por la altura del cuadrado, ya que al ser ambas iguales, el área será un lado al cuadrado.

Fórmula del área del cuadrado

La fórmula del área del cuadrado también podría obtenerse directamente de la fórmula del área del paralelogramo. En particular, si la base del cuadrado es uno de sus lados, la altura relativa a la base será un lado del cuadrado, derivando en la fórmula del área anterior.
PERÍMETRO
El cuadrado tiene los cuatro lados iguales, por lo que su perímetro es cuatro veces uno de sus lados.

RECTÁNGULO
Un rectángulo es un polígono con cuatro lados (cuadrilátero) siendo éstos iguales dos a dos. Además, sus cuatro ángulos interiores son rectos (de 90º).

Elementos y propiedades del rectángulo
- Lados: tiene cuatro lados, siendo cada lado igual a su opuesto (a y b), es decir, dos a dos.
- Ángulos: sus cuatro ángulos (α) son iguales y rectos de 90º (π/2 radianes). Los ángulos interiores, como en todo cuadrilátero, suman 360º (2π radianes).
- Diagonales: las diagonales son segmentos que unen los vértices opuestos. Tiene dos diagonales (D1 y D2) iguales y que se cortan en el centro del rectángulo.
- Ejes de simetría: son líneas imaginarias que dividen el rectángulo en dos partes simétricas respecto a dicho eje. Tiene dos ejes de simetría (E1, E2) paralelos a los lados a y b y pasan por el centro del rectángulo.
Un caso particular de rectángulo es el cuadrado, cuando todos los lados son iguales (a=b).

Diagonal del rectángulo
La diagonal del rectángulo (D) se puede calcular a partir de la longitud de los lados diferentes (a y b). La fórmula para calcular la diagonal es:

Ésta fórmula se obtiene directamente de la ley del paralelogramo.
También podría obtenerse también a partir del teorema de Pitágoras, ya que dos lados (a y b) consecutivos del rectángulo y la diagonal forman un triángulo rectángulo.

Área del rectángulo
El área del rectángulo se calcula a partir de los dos lados diferentes (a y b). Es el producto de los dos lados contiguos del rectángulo
 .
.
Esta fórmula también podría obtenerse de la fórmula del área del paralelogramo. Si la base del rectángulo es uno de sus lados (en este caso b) , la altura relativa a la base será el lado a, y aplicando la fórmula anterior obtendríamos la del área del rectángulo.
Perímetro del rectángulo
El perímetro del rectángulo es la suma de sus cuatro costados. Como el rectángulo tiene los costados iguales dos a dos, su perímetro será el doble de la suma de dos lados contiguos (es decir, a y b).

TRIANGULO
Un triángulo es un polígono de tres lados (a, b y c). Los lados confluyen dos a dos en tres puntos, llamados vértices (A, B y C).
Los tres ángulos interiores del triángulo suman 180º (π radianes).

Elementos de un triángulo
En un triángulo se pueden diferenciar los siguientes elementos:
- Dibujo de los elementos de un triángulo
- Vértices: puntos en los que confluyen dos lados. Tiene 3 vértices (A, B y C).
- Lados: segmentos que unen dos vértices consecutivos del triángulo y que delimitan su perímetro. Tiene 3 lados (a, b y c).
- Ángulos interiores: ángulo que forman dos lados consecutivos en el vértice en el que confluyen. Hay 3 ángulos interiores (α, β y γ). Los ángulos interiores del triángulo suman 180º

Ángulos exteriores: ángulo de un lado con la prolongación exterior del lado consecutivo. Hay 3 ángulos exteriores (θ). Los ángulos exteriores siempre suman 360º.
Tipos de triángulos según sus lados

Triángulo equilátero: tiene todos sus lados iguales. Por tanto, sus ángulos también son los tres iguales. Es decir:

Como todos los ángulos son iguales y suman 180º, todos son de 60º (α=β=γ=60º).

Triángulo isósceles: tiene dos lados iguales. Por lo tanto, dos de sus ángulos también son iguales.

El ángulo desigual β es el que forman los dos costados iguales (a y c).

Triángulo escaleno: los tres lados son desiguales, por lo que los tres ángulos también son diferentes. Es decir:

Tipos de triángulos según sus ángulos
- Triángulo rectángulo: uno de sus ángulos es de 90º. Los otros dos son agudos (menores de 90º).
- Triángulo acutángulo: los tres ángulos son agudos (menores de 90º).
- Triángulo obtusángulo: uno de sus ángulos es mayor a 90º. Los otros dos son agudos (menores de 90º).

ROMBO
Un rombo es un polígono con cuatro lados (cuadrilátero) siendo los cuatro iguales. Tiene cuatro ángulos interiores iguales dos a dos.

Elementos y propiedades del rombo

- Lados: el rombo tiene cuatro lados (a) iguales.
- Ángulos: tiene cuatro ángulos (dos α y dos β) iguales dos a dos. Los ángulos interiores, como en todo cuadrilátero, suman 360º (2π radianes).
- Diagonales: las diagonales son segmentos que unen los vértices no consecutivos. Tiene dos diagonales (D y d) desiguales y perpendiculares. Se cortan en el centro del rombo. Las diagonales son las bisectrices de los ángulos. También son ejes de simetría.
- Ejes de simetría: son líneas imaginarias que dividen el rombo en dos partes simétricas respecto a dicho eje. Tiene dos ejes de simetría (E1, E2) que coinciden con las diagonales.
- Un caso particular de rombo es el cuadrado, donde todos los ángulos son iguales (es decir, (α=β). Los ángulos serán todos rectos (de 90º) y las diagonales iguales.
Diagonales del rombo
El rombo tiene dos diagonales (D y d) perpendiculares y que se cortan en el centro del rombo. D es la diagonal mayor y d la diagonal menor.
Existe una fórmula que relaciona las diagonales del rombo y uno de sus lados (a). La relación es la siguiente:

Ésta fórmula se obtiene directamente de la llamada ley del paralelogramo.
También podría obtenerse también a partir del teorema de Pitágoras, ya que la mitad de cada una de las diagonales (D/2 y d/2) y un lado del rombo forman un triángulo rectángulo.

Área del rombo
Existen varias fórmulas para calcular el área del rombo. La más común es mediante las dos diagonales del rombo. El área es la mitad del producto de las diagonales (D y d).

.
Otra forma de calcular el área del rombo es mediante la fórmula del área del paralelogramo.
En este caso, un lado (a) se considera la base del rombo. Se mide la altura (h) relativa a dicha base, de manera que el área será el producto de la base por la altura.

Perímetro del rombo
El rombo tiene sus cuatro lados iguales, por lo que su perímetro es cuatro veces la longitud de uno de sus lados (a).

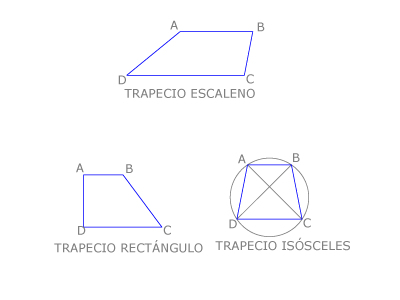
TRAPECIO
Los trapecios son cuadriláteros convexos con un par de lados paralelos a los que llamamos bases. Sus diagonales nunca se cortan en el punto medio. Solamente son inscriptibles los trapecios isósceles, que son los que tienen los dos lados no paralelos iguales
Propiedades y trazados generales
- Propiedad 1
Si trazamos una paralela a un lado por un extremo de la base menor, el trapecio queda dividido en un paralelogramo cuyos lados son la base menor y dicho lado y en un triángulo cuyos lados son la diferencia de las bases y los dos lados del polígono.
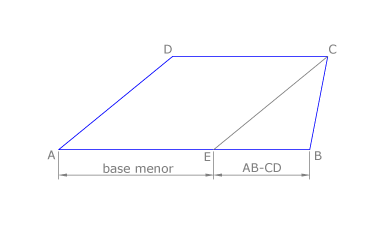
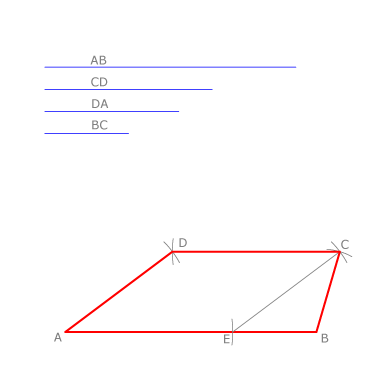
En esta propiedad nos basamos para construir un trapecio cuando se conocen sus bases y sus lados: se dibuja la base mayor AB y se le resta la menor CD. Se dibuja el triángulo de lados la diferencia de las bases EB y los lados AD y BC del trapecio. Así se halla C.
Se trazan arcos de centro en C y radio CD y de centro en A y radio AD en cuya intersección está el punto D.
- Propiedad 2
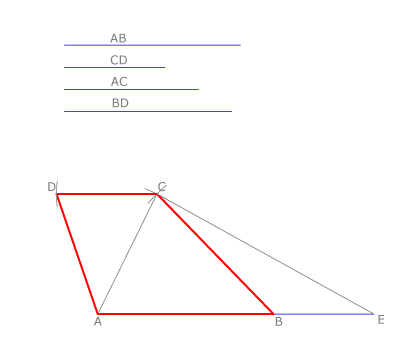
Si trazamos una paralela a una diagonal por un extremo de la base menor y dibujamos la base menor a continuación de la mayor se forma un triángulo cuyos lados son la suma de las bases y las dos diagonales del polígono.
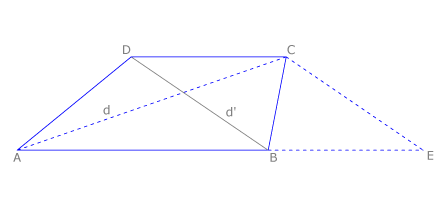
En esta propiedad nos basamos para construir un trapecio cuando se conocen sus bases y sus diagonales: se dibuja la base mayor AB y se le suma la menor CD. Se dibuja el triángulo de lados la suma de las bases AE y las diagonales AC y BD del trapecio. Así se halla C.
Se trazan arcos de centro en C y radio CD y de centro en A y radio AD en cuya intersección está el punto D.
- Propiedad 3
En los trapecios se llama altura a la distancia entre las bases, la cual se representa con "h"
- Propiedad 4
Si se prolongan los lados de un trapecio se forma un triángulo que tiene en común con el trapecio un lado, la base mayor y los ángulos apoyados sobre ella.
Triángulo equivalente a un trapecio
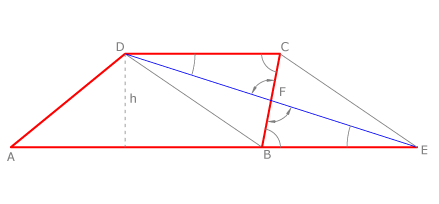
Todo trapecio es equivalente a un triángulo que tenga como base la suma de las bases y como altura respecto de ella la misma altura del trapecio.
En general se considera altura del trapecio a la distancia entre las bases.
Vamos a comprobarlo gráficamente. En la figura consideramos el trapecio ABCD y el triángulo ADE. Vemos que tienen una parte común, el cuadrilátero ABFD.
Por lo tanto bastará con comprobar que los triángulos FBE y DCF son iguales, lo que es evidente: DC=BE, CF=FB y DF=FE, por ser BECD un paralelogramo
PENTÁGONO
Un pentágono es un polígono de cinco lados y cinco vértices.

Ángulos del pentágono
Suma de ángulos interiores de un pentágono = (5 − 2) · 180° = 540°
El valor de un ángulo interior del pentágono regular es: 540º : 5 = 108º
El ángulo central del pentágono regular mide: 360º : 5 = 72º
Diagonales del pentágono
Número de diagonales = 5 · (5 − 3) : 2 = 5

Apotema del pentágono regular


Perímetro de un pentágono regular
Perímetro = 5 · l

Área de un pentágono regular

No hay comentarios:
Publicar un comentario